Twin Primes Follow up V4
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 3/8/2024
- Twin Primes Follow up V4
- Preface
- Introduction
- Not a Replacement for TCL Core
- Body
- Draft Outline for Applications of Primes including Twin Primes
- Extension of Historical Gauss, Legendre, and Modified_Legendre approximations
- Testing Digit 3 is Everywhere using One Line Procedure
- Testing Mill's Constant for Primes using One Line Procedure
- Pseudocode on Tcllib listPrimePairs
- Math Template Subroutine for study here
- Gaps between Twin Primes, What expected?
- Table: Rarity of Primes as percent reported from Modified_Legendre_primes function
- References:
- Extra Credit on One Line Procedures
- Screenshots Section
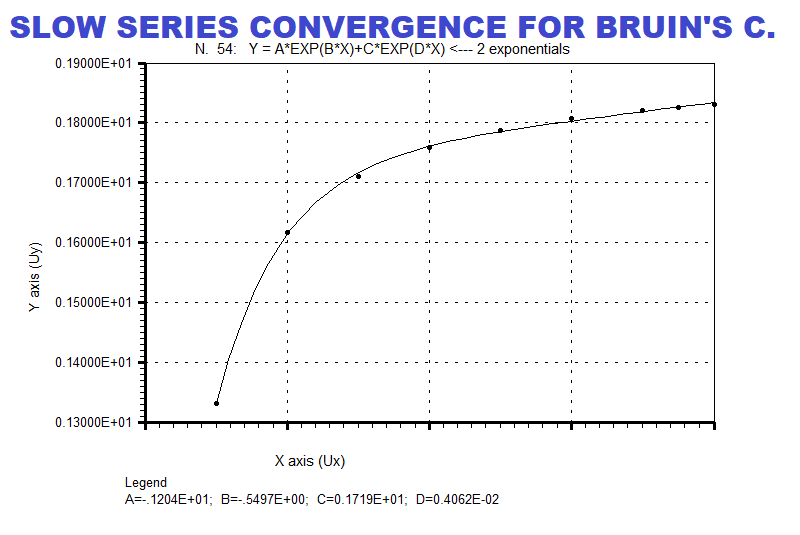
- figure 1. Slow Series Convergence for Brun Constant
- figure 1a. Bruns constant in lower primes field
- figure 1c. Bruins constant series
- figure 1d. Twin Primes Follow up with Pseudocode extra chart on brun constant no2
- figure 1e. Twin Primes Follow up with Pseudocode Primes and Twin Primes
- figure 1f. Twin Primes Follow up with Pseudocode Study Gauss Li(x) function
- figure 2.
- figure 3.
- figure 4.
- figure 5.
- figure 6.
- figure 7.
- figure 8.
- figure 9.
- figure 10.
- figure 11.
- figure 12.
- The Arakarum Operator Stage is found in some Babylonian Algorithms
- Hidden Comments Section
Twin Primes Follow up V4
Preface
gold Update 3/7/2024. The Twin Primes procedure is loaded on the Tcllib math::primes module. Reference Routines are listPrimePairs and listPrimeProgressions on Tcllib. Study of Twin Primes features using pseudocode. One can add a counting function for the Tcllib listPrimePairs procedure to generate the Twin Primes Counting Function. Likewise, one could rig up a counting function for the Tcllib listPrimeProgressions function and generate a Counting Function for those sets. Console program outputs data as table in TCL table format and comma delimited spreadsheet. These auxiliary decks are used to proof features or subroutines. The Monopoly page from GWM seems closest in theme to what I was trying to learn. Using dice and running with random throws along a track or path like Snakes and Ladders.
gold Update 3/7/2024. The author is retired engineer on Windows 10 and no longer has proofing access to Unix machines. Unix is respected after use of so many decades in engineering, but my wings are lost. I did find a useful online IDE, jdoodle. I can paste from a text file, edit, and run an output using this online IDE.
gold Note: Some tickets for prime numbers are closed and functions available in Tcllib. Many thanks to Arjen Markus arjen AM & Andreas Kupries for the heavy lifting.
closer: arjenmarkus AM
Emailed comment from AM: I used the sample code to create two new procedures:
listPrimePairs listPrimeProgressions
The first proc listPrimePairs returns a list of pairs of primes that differ by a given number and the second proc listPrimeProgressions returns a list of arithmetic progressions of primes that differ by the given number.
Introduction
Not a Replacement for TCL Core
This page on developing pseudocode examples and one line procedures is not a replacement for the current Tcl core and Tcllib, which is much improved since Tcl version 4, and other <faster> language constructs. math ops, Tcllib routines, and other compiled routines can reduce the cost of big-data tasks by about 1/3. The time savings of the core are not always obvious on small quantities of data, like 4 or 5 numbers. Performance of one-line programs may suffer degradation due to lengthy recursion calls, and may be limited by constraints on recursion. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines.
gold 3/8/2024 Draft & Check.
Body
Draft Outline for Applications of Primes including Twin Primes
1. Cryptography: Primes play a crucial role in encryption algorithms such as RSA (Rivest-Shamir-Adleman), which relies on the difficulty of factoring large numbers into their prime components to secure communication online.
2. Number theory: Primes are fundamental in number theory, the branch of mathematics that studies the properties and relationships of numbers. Studying prime numbers helps to understand the distribution of primes, prime factorization, and other important concepts in mathematics.
3. Primality testing: Algorithms have been developed to efficiently determine whether a given number is prime. These algorithms are essential in various applications, such as programming languages, cryptography, and computer science.
4. Random number generation: Primes are often used in generating random numbers, especially in cryptographic applications where randomness is crucial for security. The use of prime numbers in random number generation ensures a higher level of unpredictability and security.
5. Error detection and correction: Primes are used in error detection and correction algorithms, such as the Reed-Solomon codes, which are commonly used in data storage and transmission systems. By leveraging the properties of prime numbers, these algorithms can detect and correct errors in transmitted data.
Twin primes, which are prime numbers that have a difference of 2 (e.g., 3 and 5, 11 and 13), have applications in number theory, cryptography, and computer science.
1. In number theory, the study of twin primes helps researchers understand the distribution of prime numbers. Interestingly, there’s a pattern: all twin prime pairs, except the first one (3, 5), follow the form {6n-1, 6n+1}.
2. In cryptography, twin primes are used in certain encryption algorithms.
3. In computer science, twin primes can be used in algorithms for generating random numbers. In 1994 American mathematician Thomas Nicely was using a personal computer equipped with the then new Pentium chip from the Intel Corporation when he discovered a flaw in the chip that was producing inconsistent results in his calculations of Brun’s constant for twin primes.
Extension of Historical Gauss, Legendre, and Modified_Legendre approximations
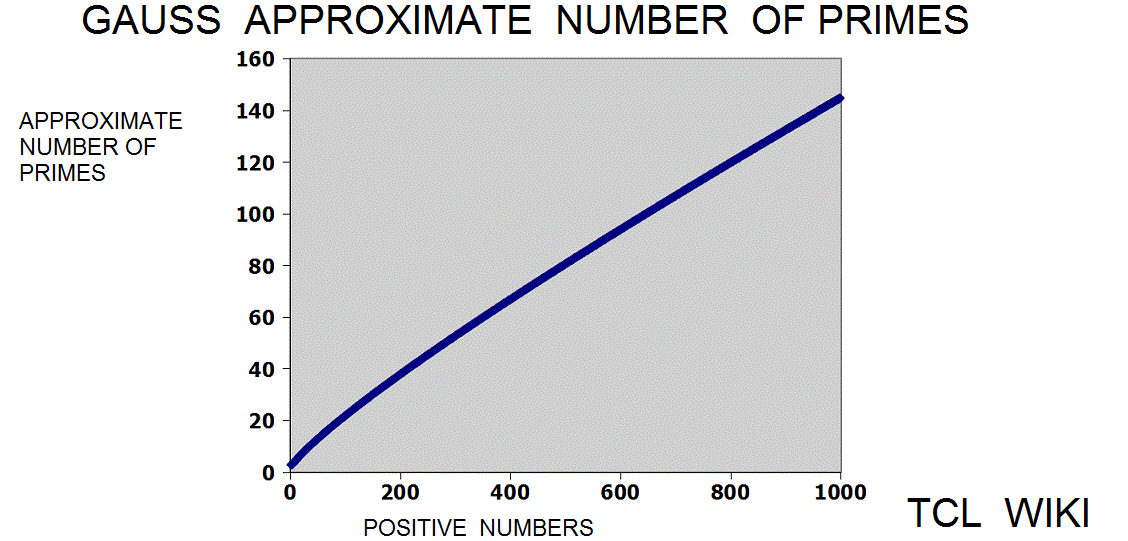
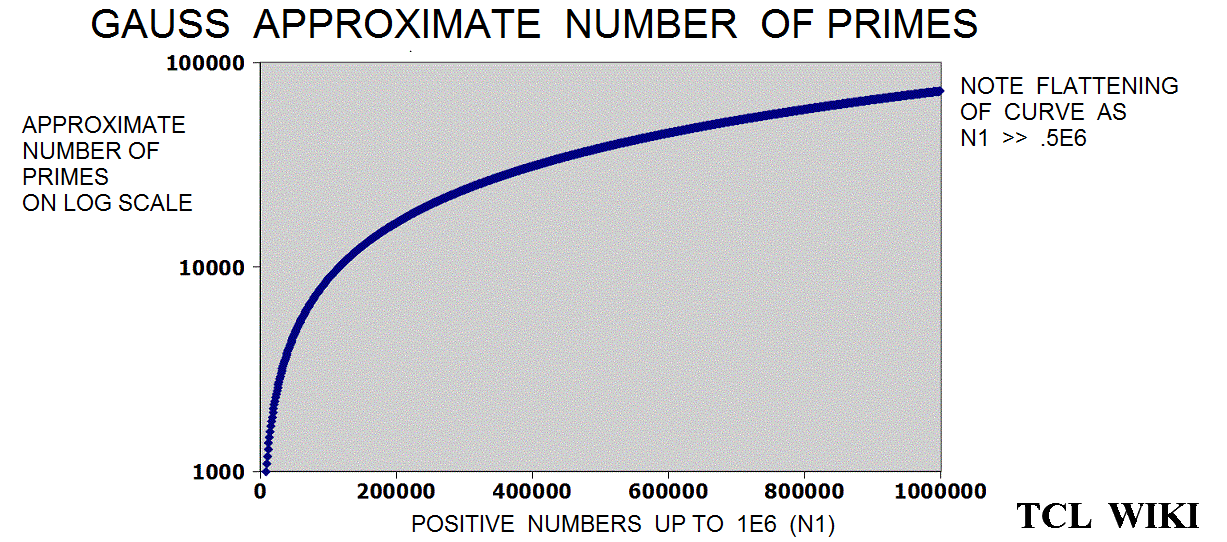
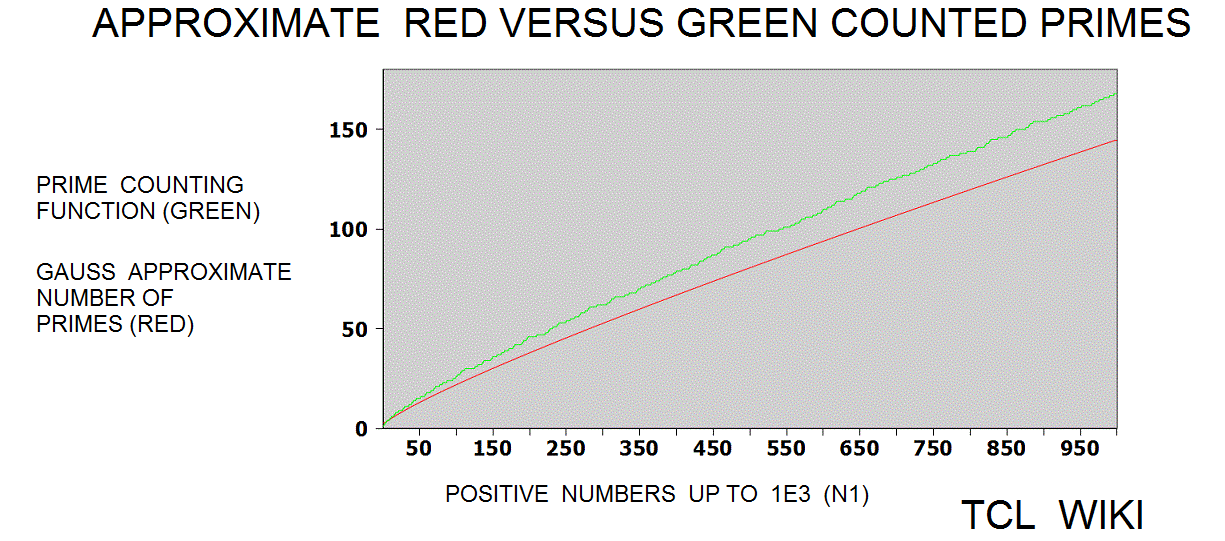
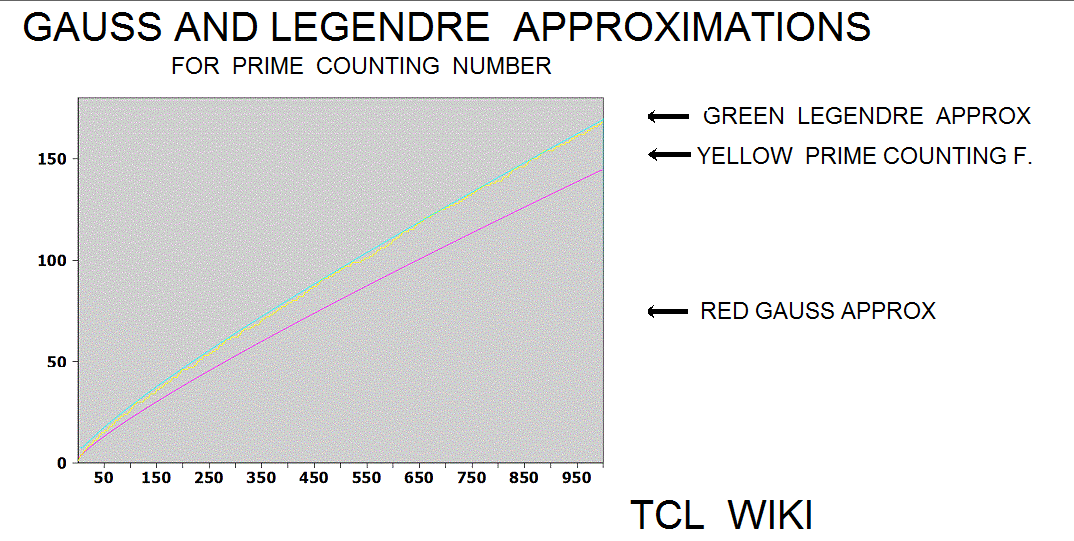
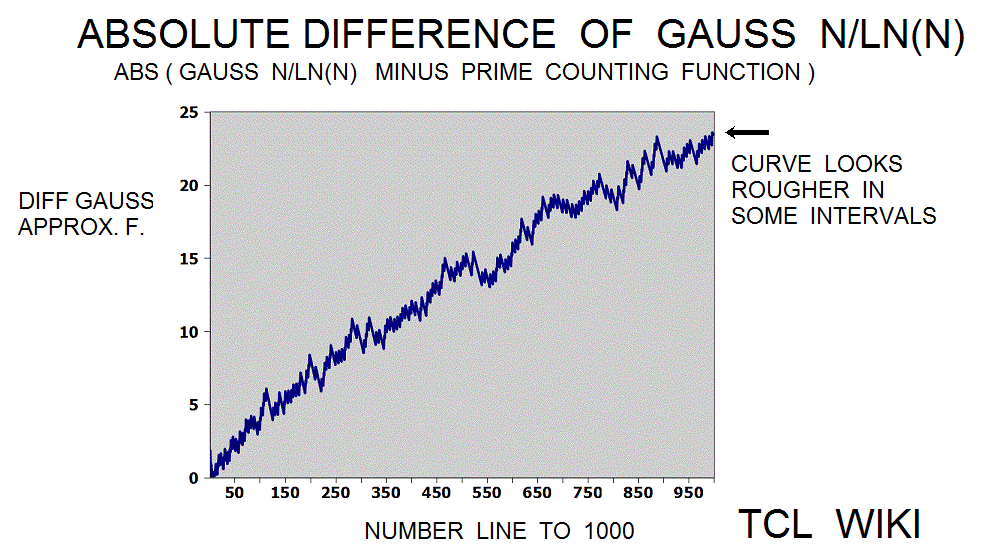
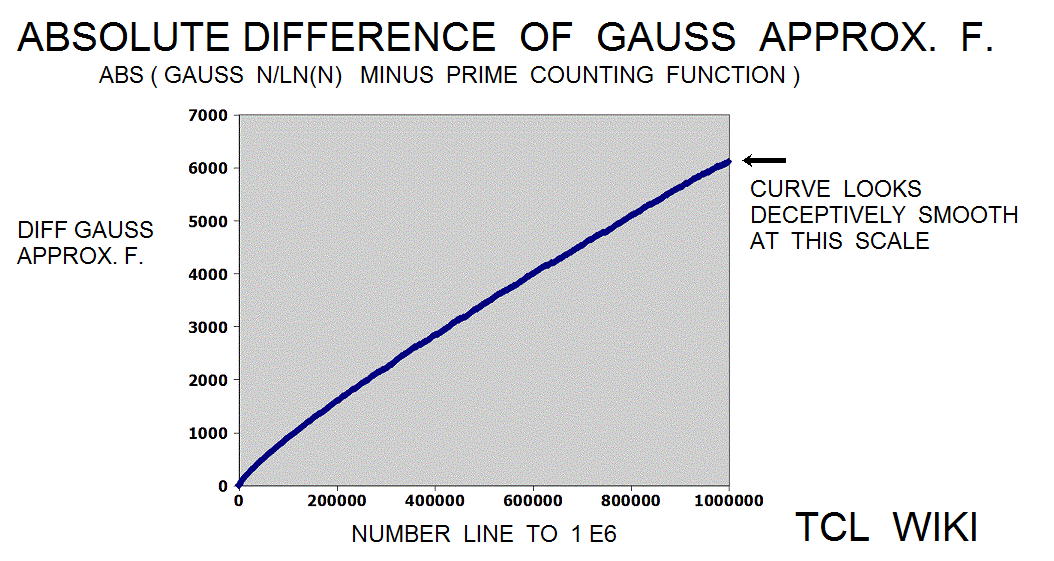
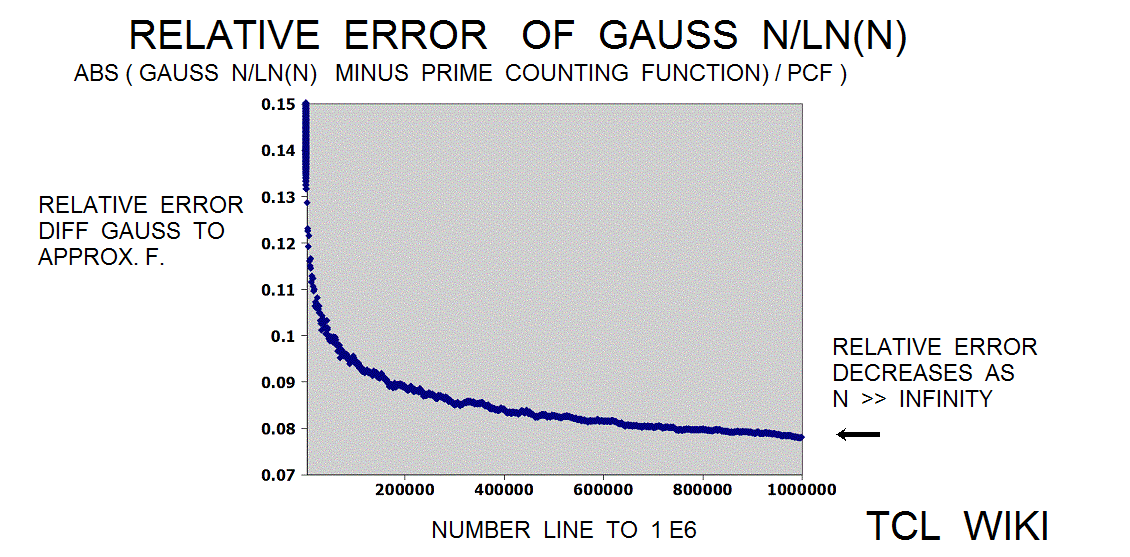
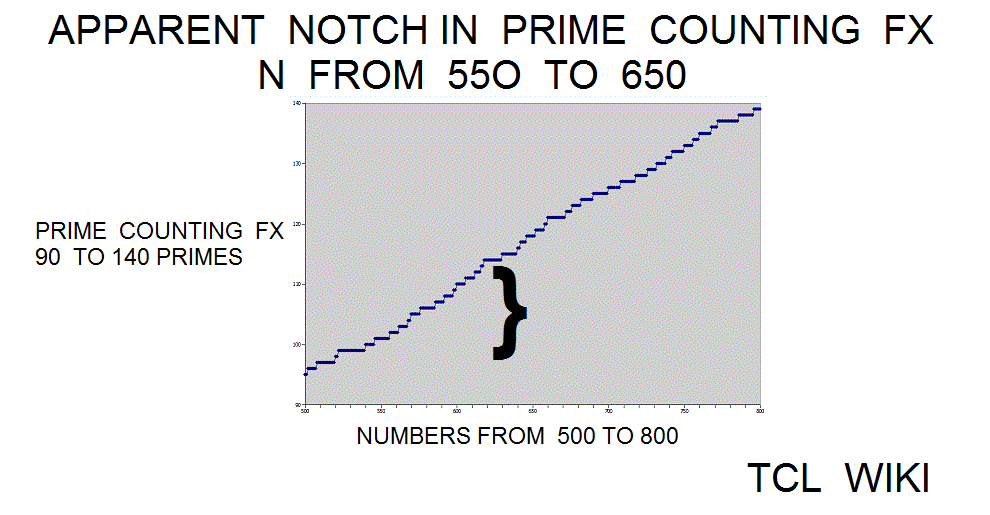
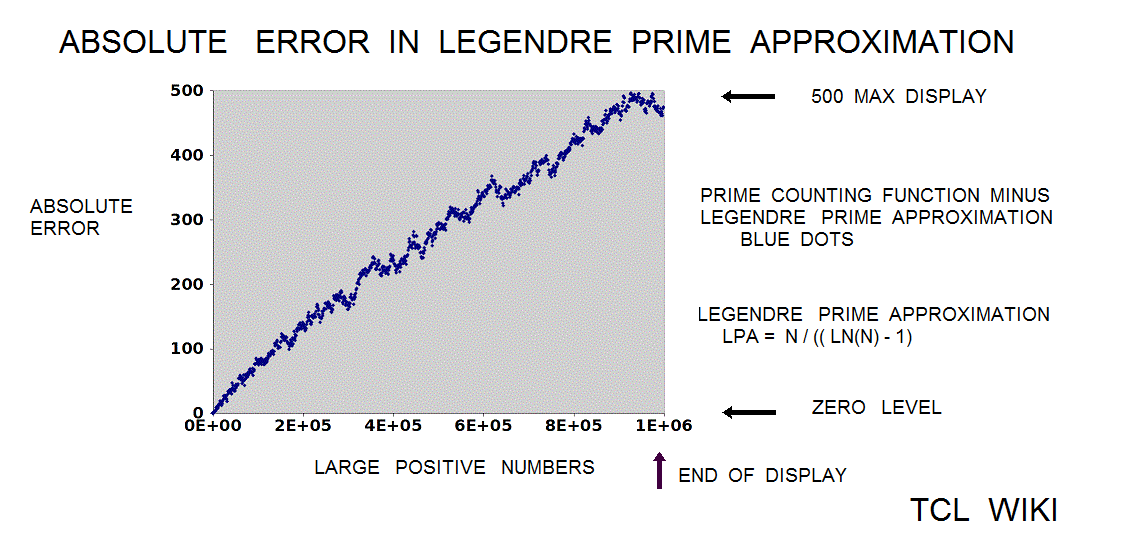
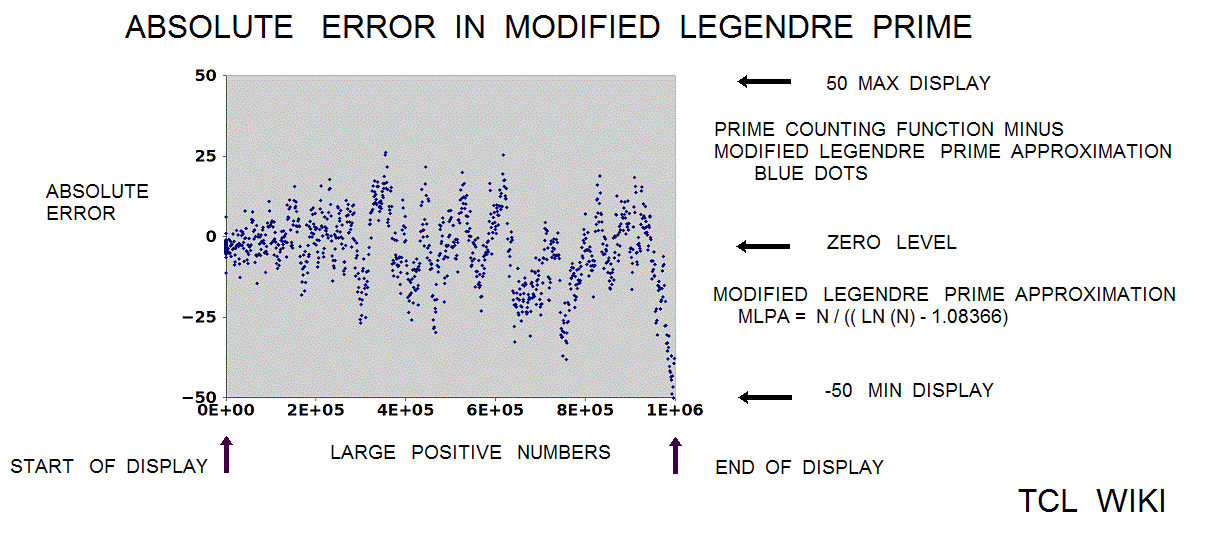
Extension of Historical formulas. In an 1849 letter, Gauss discussed findings on the number of primes in various regions of the number line. The historical background of this prime number theory is of interest today in developing simple TCL routines. The Gauss approximation for number of primes is approx_number_primes = N1 / ln (N1), 15 percent average error. Gauss developed this formula at the age of 14! and formula was first published in 1863. If the exact solution is tabbed as one, the program is storing the exact solution in a list of limited size. The number one should not be counted as a prime and the number two is counted as prime, so some starting algorithm statements are tricky. The Legendre approximation for number of primes was approx_legendre_primes2 = N1 / (ln (N1)-1), 2 percent average error beyond 1E4. A variant of the Legendre equation was modified_legendre_primes3 = N1 / (ln (N1)-1.08366). In the modified Legendre error covering E6, no particular trends are seen leading from zero level, but there are some sawtooth patterns at intervals. Also the prime counting function is reported to have gaps between the primes, which might be difficult to see at this density.
in 1922, by Godfrey Harold Hardy (1877-1947) and John Edensor Littlewood (1885-1977) to estimate the density of twin primes. Starting with the Gauss approximation and the Hardy paper, the probability that a number n is prime is about 1/log(n). Therefore, if the probability that n+2 as a prospective twin prime is also prime was independent of the probability for n. The approximation for the prime density PI2 of twin primes PI2(n) ~~ n/(log(n)*log(n).
Extension. If one starts with the modified_legendre_primes3 = N1 / (ln (N1)-1.08366) and similar postulates as before. Then possibly an approximation for the twin prime density would be = N1 / ((ln (N1)-1.08366) * (ln (N1)-1.08366)) ? The extension formula could be developed into a one line procedure in TCL. The modified Legendre approximation reported about 28 primes from field of 0 to 100. The modified Legendre approximation reported about rounded 8 pairs of twin primes from field of 0 to 100. The Tcllib program reported 8 sets of twin primes over the interval of 100 as list of twin primes = {3 5} {5 7} {11 13} {17 19} {29 31} {41 43} {59 61} {71 73}.
Testing Digit 3 is Everywhere using One Line Procedure
Ref. = 3 is everywhere - Numberphile
"almost all very large numbers contain the digit 3"
T(n+1) = 10^n -9^n
ratio of T(n+1) / 10^n = ( 10^n-9^n)/10^n = 1-(9/10) = 1/10 at infinity
ratio of number with digit 3 to all positive numbers
ratio goes to 1 at infinity
primes can not be even numbers > 2
N1>10, primes end in either 1,3,5,7 for base 10?
# testing on fly
# probability that a large number will have the digit 3.
# ratio of numbers with digit 3 to all positive numbers at set $limit
# need some test cases.
proc probabability_no3_tester {limit} { expr { ((1*1.)/10)*$limit }}
puts " probabability_no3_tester 321 = [ probabability_no3_tester 321 ] "Testing Mill's Constant for Primes using One Line Procedure
# Power formula produces a prime number from Mill's Constant
global theta
set theta 1.3063778838630806904686144926
proc mills_constant_tester {limit} { global theta;
expr { int( [ expr {($theta**(3**$limit))} ] )}}
puts " mills_constant [ mills_constant_tester 1 ] "
puts " mills_constant [ mills_constant_tester 2 ] "
puts " mills_constant [ mills_constant_tester 3 ] "
puts " mills_constant [ mills_constant_tester 4 ] "
# mills_constant 2
# mills_constant 11
# mills_constant 1361
# mills_constant 2521008886
# big numbers evaled and large significant figures in constant, results limited quickly in most setups. Note. Power formula produces a prime number from Mill's Constant. Big numbers are evaled here and large significant figures in constant. Results are limited quickly in most setups.
Note. Condition on primes that N>10, primes end in either 1,3,5,7 for base 10? In base 10, prime numbers end in either 1, 3, 7, or 9. The last digit of a prime number cannot be 0, 2, 4, 6, or 8 because those numbers are all divisible by 2. The last digit cannot be 5 because that would make the number divisible by 5. This leaves us with the last digits 1, 3, 7, and 9.
Pseudocode on Tcllib listPrimePairs
# Pseudocode
# Procedure: listPrimePairs
# Note dependency here on Tcllib proc isprime
# Parameters:
# lower - lower limit for the interval
# upper - upper limit for the interval
# step - difference between successive primes (default: 2)
# Return:
# list of pairs of primes differing the given step
# Procedure is_prime to check if a number is prime
proc is_prime(n):
if n < 2:
return False
for i from 2 to sqrt(n):
if n % i == 0:
return False
return True
# Procedure listPrimePairs
procedure listPrimePairs(lower, upper, step=2):
# Validation card
if upper <= lower:
return error: "The upper limit must be larger than the lower limit"
if step <= 0:
return error: "The step must be at least 1"
# Initialize output variable here, list in TCL
output = []
# for next loop in TCL
for i in range(lower, upper+1):
next = i + step
if isPrime(i) and isPrime(next):
output.append([i, next])
return output
EndPseudocode generates a list of prime number pairs that differ by the given step within the specified interval. The pseudocode uses a similar logic to the original Tcllib script, with some minor modifications to match the pseudocode syntax.
One can add a counting function for the Tcllib listPrimePairs procedure to generate the Twin Primes Counting Function. Likewise, one could rig up a counting function for the Tcllib listPrimeProgressions function and generate a Counting Function for those sets.
# ... Tcllib program listing ...
# set goofy 0
# set goofy [ expr { $goofy + 1 } ] # in the twin primes loop
puts " goofy counter for twin primes counting function [expr { $goofy} ] "
return $output
}
puts " list of twin primes = [ listPrimePairs 3 50 2 ] "
# output
goofy counter for twin primes counting function 6
list of twin primes = {3 5} {5 7} {11 13} {17 19} {29 31} {41 43} # list from copy of [Tcllib] deck on jdoodle.
brun constant over selected range =
series 1/5 + 1/7 + 1/11 + 1/13 + 1/17 + 1/19 + 1/29 + 1/31 + 1/41 + 1/43 + 1/59 + 1/61 = 0.7698738952
puts " list of twin primes = [ listPrimePairs 3 100 2 ] "
list of twin primes = {3 5} {5 7} {11 13} {17 19} {29 31} {41 43} {59 61} {71 73}
brun constant over selected range 0.5333333333333333
brun constant over selected range 0.5333333333333333
brun constant over selected range 1.330990365719087
brun constant over selected range 1.330990365719087
puts " list of twin primes = [ listPrimePairs 3 500 2 ] "
bruin constant over selected range 1.486060792020912
brun very slow closer and not much core allowance on jdoodle
monograph = B2(p = 10**16) = 1.902160583104
series converges extremely slowly.Reference Testcases
Test Cases P -> Partial Sum of series for Brun Constant 2 -> 0 6 -> 0.5333333333333333 10 -> 0.8761904761904762 13 -> 0.8761904761904762 100 -> 1.3309903657190867 620 -> 1.4999706034568274 100000 -> 1.67279958482774 p B2(p) 10E2 1.330990365719 10E4 1.616893557432 10E6 1.710776930804 10E8 1.758815621067 10E10 1.787478502719 10E12 1.806592419175 10E14 1.820244968130 10E15 1.825706013240 10E16 1.830484424658 different more converging formula? Ref = Introduction to twin primes and Brun’s constant computation Pascal Sebah and Xavier Gourdon 10^5: 1.90216329186 ( 6.1 s) 10^6: 1.90191335333 ( 63.1 s) 10^7: 1.90218826322 ( 759.6 s) 2*10^7: 1.90217962170 (1692.3 s) B2(p = 10**16) => 1.902160583104
Math Template Subroutine for study here
Gaps between Twin Primes, What expected?
The first 60 prime gaps are:
1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14, 4, 6, 2, 10, 2, 6, 6, 4, 6, 6, 2, 10, 2, 4, 2, 12, 12, 4, 2, 4, 6, 2, 10, 6, 6, 6, 2, 6, 4, 2, ... (sequence A001223 in the OEIS).
The average gap between primes increases as the natural logarithm of these primes, and therefore the ratio of the prime gap to the primes involved decreases (and is asymptotically zero). This is a consequence of the prime number theorem. --- Wikipedia
Taking averages between prime pairs, the positions of 2. what expected?
mean 2, 4, 6, 6, 2, mean 2, 4, 14, 4, 6, 2, mean 2, 10, 6, 6, 6, 2 puts " math_mean = [math_mean 2 4 6 6 2 ]" # 4 puts " math_mean = [math_mean 2 4 14 4 6, 2 ]" # 5 puts " math_mean = [math_mean 2 10 6 6 6, 2 ]" # 5
Table: Rarity of Primes as percent reported from Modified_Legendre_primes function
| table Rarity of Primes | mod_percent {n} | Modified Legendre P. Function | Prime Counting Function | printed in | tcl wiki format | |
|---|---|---|---|---|---|---|
| testcase | power or order | TCL proc percent from mod legendre_primes | mod legendre_primes | prime_pi | percent prime_pi | comment if any |
| testcase 1 | .5E1 | not acc. | 9.5097 not acc. | 3 | 60.0 | expr (3./5.)*100. |
| testcase 2 | 1E1 | not acc. | 8.2039 not acc. | 4 | 40. | expr (4./10.)*100. |
| testcase 3 | 1E2 | 28.397 | 28.397 | 25 | 25. | expr (25./1E2)*100. |
| testcase 4 | 1E3 | 17.17 | 171.7 | 168 | 16.8 | expr (168./1E3)*100. |
| testcase 5 | 1E4 | 12.3051 | 1230.514 | 1229 | 12.29 | expr (1229./1E4)*100. |
| testcase 6 | 1E5 | 9.5884 | 9588.402 | 9592 | 9.592 | expr (9592./1E5)*100. |
| testcase 7 | 1E6 | 7.854 | 78543.178 | 78498 | 7.8498 | f(x) =(( prime_pi (x))/x)*100. |
| testcase 8 | 1E7 | 6.651 | 665139.699 | 664579 | 6.64579 | |
| testcase 9 | 1E8 | 5.768 | 5768003.712 | 5761455 | 5.761455 | |
| testcase 10 | 1E9 | 5.092 | 50917518.829 | 50847534 | 5.0847534 | |
| testcase 11 | 1E10 | 4.557 | 455743003.601 | 455052511 | 4.55052511 | |
| testcase 12 | 1E11 | 4.125 | 4124599868.665 | 4118054813 | 4.118054813 | |
| testcase 13 | 1E12 | 3.767 | 37668527415.329 | 37607912018 | 3.7607912018 | |
| testcase 11 | 1E13 | 3.466 | 346621096884.653 | 346065536839 | 3.46065536839 | |
| testcase 12 | 1E14 | 3.21 | 3210012022164.23 | 3204941750802 | 3.204941750802 | |
| testcase 13 | 1E15 | 2.989 | 29890794226981.8 | 29844570422669 | 2.9844570422669 |
References:
Omitting outside links here, too transitory on internet.
- TCLLIB math::primes module
- Gauss Approximate Number of Primes and eTCL demo example calculator
- TCLLIB Current Release 1.21 (May 7, 2022)
- math::primes::isprime
- math::primes::firstNprimes
- math::primes::primesLowerThan
- math::primes::primeFactors
- math::primes::numberPrimesGauss
- math::primes::numberPrimesLegendre
- math::primes::numberPrimesLegendreModified
- math::primes::differenceNumberPrimesLegendreModified
- math::primes::numberPrimesLegendre N
- math::primes::numberPrimesLegendreModified N
- math::primes::differenceNumberPrimesLegendreModified lower upper
- math::primes::listPrimePairs lower upper step
- math::primes::listPrimeProgressions lower upper step
- Prime Counting functions in R, article by Charles Spackman. 2018, interesting article
- Bruin's Constant at p=10**16 , B2(p = 10**16) = 1.902160583104..
- Ref = Introduction to twin primes and Brun’s constant computation
- Pascal Sebah and Xavier Gourdon
- On-Line Encyclopedia of Integer Sequences , OEIS
- Andrew Granville, Primes in intervals of bounded length, Joint Math Meeting, Jan 17 2014.
- J. C. Evard, Twin primes and their applications, archived Pdf
- James Maynard, Small gaps between primes, arXiv:1311.4600 , 2013, Annals of Mathematics,
- Godfrey Harold Hardy (1877-1947) and John Edensor Littlewood (1885-1977)
- to estimate the density of twin primes. historic approximate formula.
- many assumptions, p2(n) ~~ n / (log(n) * log(n)) , ref Gauss formula for prime number density.
- substantial interest online codegolf_
- stackexchange /questions/107634/approximate-bruns-constant
- sagemath twin_prime constant
- The Twin Primes constant
- sage: float(twinprime)
- 0.6601618158468696
- sage: twinprime.n(digits=60)
- sage: 0.660161815846869573927812110014555778432623360284733413319448
- Improved bounds on Brun’s constant, Dave Platt, University of Bristol
- Enumeration to 1e14 of the twin primes and Brun's constant, Thomas R. Nicely
- Video References. Some Featuring Ed Copeland, Tony Padilla, James Maynard, intro by Brady Haran.
- The Reciprocals of Primes - Numberphile
- Gaps between Primes (extra footage) - Numberphile
- Twin Proofs for Twin Primes - Numberphile
- The Badly Behaved Prime (with James Maynard) - Numberphile Podcast
- Twin Prime Conjecture - Numberphile, James Maynard
- Awesome Prime Number Constant with Mills' Constant - Numberphile
- Mills constant, 1.3063778838630806904686144926... (sequence A051021 in the OEIS).
- The Sum of All Prime Twins, Bruin constant
- Ref. = 3 is everywhere - Numberphile
- "almost all very large numbers contain the digit 3"
- Wikipedia: Gambler's Ruin
- Khan Academy: Gambler's Ruin
- MathWorld: Gambler's Ruin
- Wolfram Alpha: Gambler's Ruin Problem
- Quora: What are some practical applications of the Gambler's Ruin Problem?
- The Gambler's Ruin Problem" - Discrete Mathematics with Applications, by Kenneth Rosen:
- A chapter from the textbook explaining the Gambler's Ruin Problem
- and its applications in discrete mathematics
- "The Gambler's Ruin Problem: A Case Study in Probability" - MIT OpenCourseWare:
- A lecture on the Gambler's Ruin Problem
- "The Gambler's Ruin Problem" - Khan Academy: A video lesson explaining
- the Gambler's Ruin Problem and its applications in probability and statistics.
- Category Algorithm
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Taking a Weighted Average, Dr Math, mathforum.org/dr.math, dated 03/20/2003
- google <Weighted Average, Dr Math>, mathforum.org/dr.math
- Using Weighted Criteria to Make Decisions, Dr Math>, mathforum.org/dr.math, dated 07/18/2008
- google <Weighted sum product model Decision >
- harmonic mean discussed in Additional math functions
- harmonic mean discussed in Tcl Normalized Extended Benchmarks
- see arithmetic mean on tcl-wiki Stats 2011-05-22, RLE
- see similar 1/(1/nth) terms method used in
- Babylonian Combined Market Rates and eTCL demo example calculator, numerical analysis
- GoDuck search engine < Functional Programming >
- GoDuck search engine < Imperative Programming >
- GoDuck search engine < Programming Examples >
- Google search engine < vaporware >
- Tcllib math::special Special mathematical functions
- Tcllib math::figurate Evaluate figurate numbers
- Tcllib simulation::random Pseudo-random number generators
- Tcllib simulation::montecarlo Monte Carlo simulations
- Wikipedia search engine < Lehmer random number generator >
- Professor Frisby's Mostly Adequate Guide to Functional Programming on internet archive
- Writing code using the Pseudocode Programming Process, article by David Zych
- Mathematical Methods in Large-scale Computing Units
- by Derrick H. Lehmer
- L’Ecuyer, Pierre (January 1999). "Tables of linear congruential generators of different sizes and good lattice structure"
- Mathematics of Computation. 68
- A Comprehensive Review of Quantum Random Number PDF
- Good Pedagogical Random Number Generators
- from J. Stanley Warford
- Coding the Lehmer Pseudo random Number Generator
- from W. H. PAYNE
- The most commonly used version of the Mersenne Twister algorithm
- is based on the Mersenne prime expr { 2**19937-1 }
- TWISTER = 431542479738816264805523551633791983905393504322.....
- GoDuck search engine < TCL version >
- One Liners Programs Pie in the Sky
- One Liners
- One Liners Programs Compendium [L1 ]
- WIKI BOOKS, Programming_Examples pdf
- WIKI BOOKS, Tcl_Programming_Introduction pdf
- Note. I did find a useful online IDE, jdoodle
- Note. I can paste, edit, and run an output using this online IDE.
- How Do I Write Pseudocode? video by Mr. Brown CS
- Refers to rand, RandMT, Mersenne Twister, & random
- Suchenworth RS on Horseracing in Tcl.
- Random Number Generators: Good Ones Are Hard to Find, Keith Willam Miller, pdf online
- Throwing Two Dice GWM and Dice by Keith Vetter.
- int from RLE has dice expression expr {1 + int(rand()*6)} RLE.
- Several Dr. Math emails may reduce some dice issues to simple paths, internet archive.
- Counting Elements in a List from RWT.
Extra Credit on One Line Procedures
- Little L Programming Language
- Let's assign with let
- let
- let2
- Easy Eye Calculator [L2 ]
- Tcl the Misunderstood
- Maximum nummeric value from max
- L-Language pdf L , by Larry McVoy:
- One liners Programs Pie in the Sky
- Counting characters in a string
- Playing with recursion
- recursive functions
- If we had no expr
- expr
- little language
- string is
- Wikipedia search engine < random >
- Wikipedia search engine < dice >
- Wikipedia search engine < Programming Examples >
- Google search engine < vaporware >
- One Liners Programs Pie in the Sky
- One Liners
- One Liners Programs Compendium [L3 ]
- WIKI BOOKS, Programming_Examples pdf
- WIKI BOOKS, Tcl_Programming_Introduction pdf
- google search engine < HgA1c to Average Blood Glucose>
Screenshots Section
figure 1. Slow Series Convergence for Brun Constant
gold Off the cuff, that double exponential curve fit seems to be tracking fairly well.
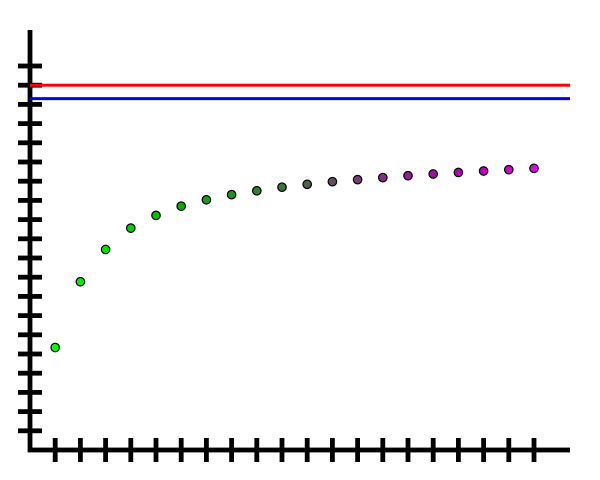
figure 1a. Bruns constant in lower primes field
Credit to Wikipedia-(Kiwi128) Bruns constant in lower primes field. The convergence to B2. Each dot represents the effect of an additional pair of twin primes. While the exact value of B2 is unknown, it is thought to be around 1.9 (red line). Calculations have shown it to be greater than 1.83 (blue line)
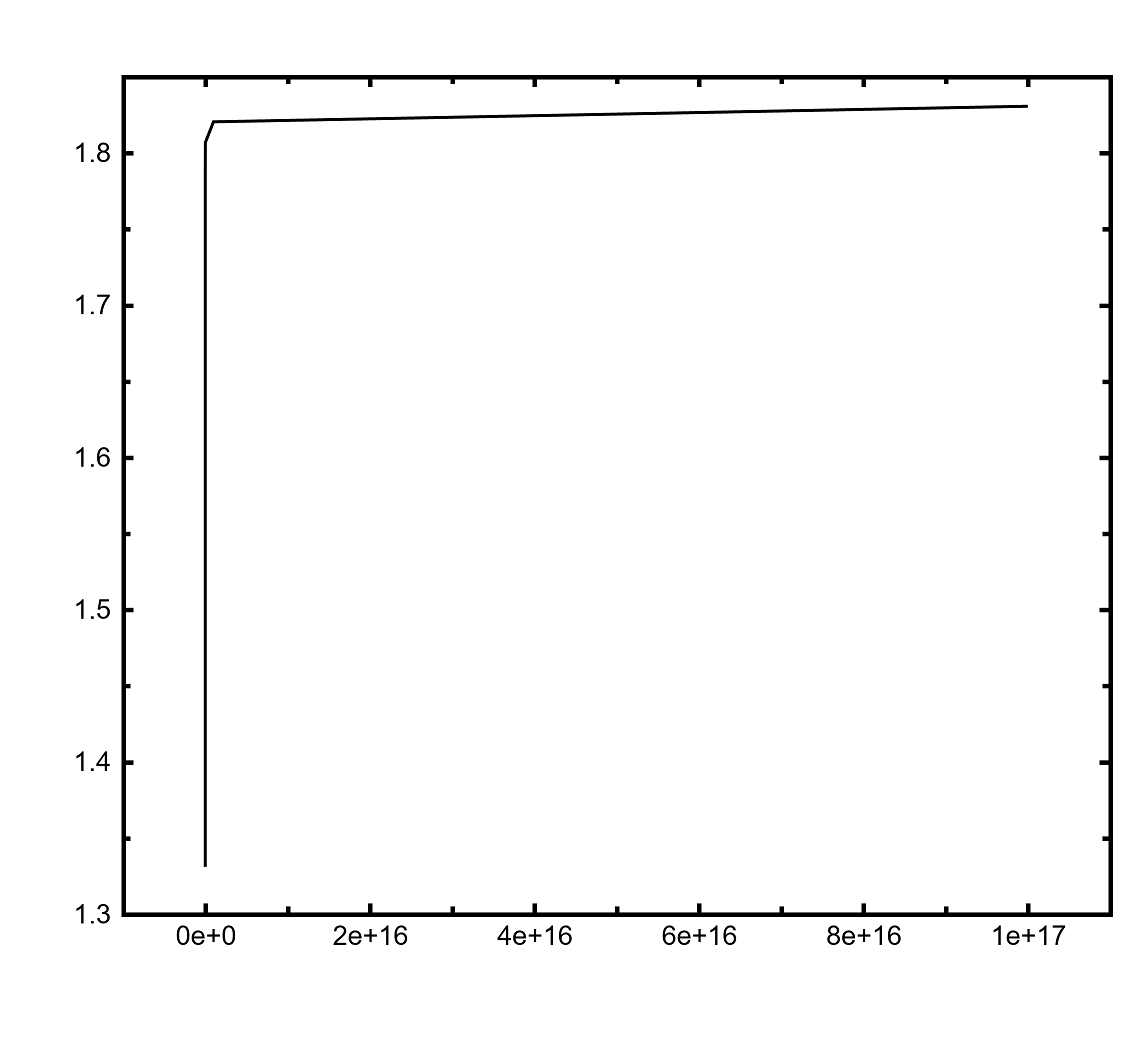
figure 1c. Bruins constant series
Number theory - 2018-08-08, chat.stackexchange.com
figure 1d. Twin Primes Follow up with Pseudocode extra chart on brun constant no2
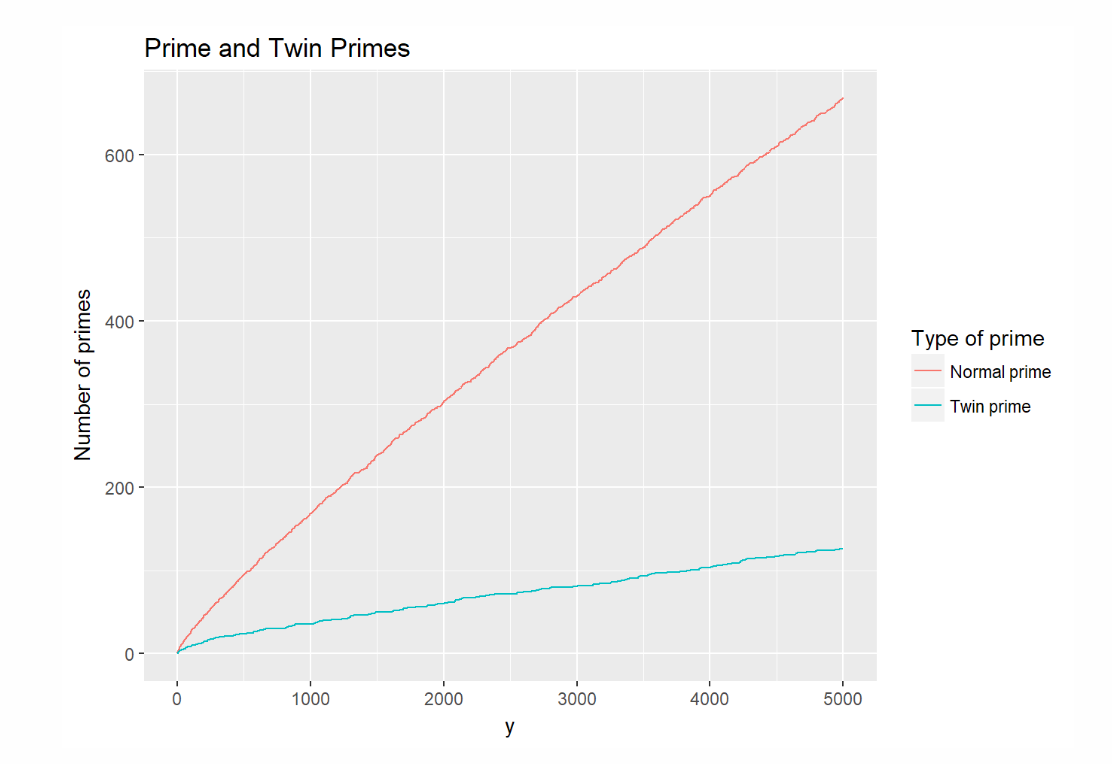
figure 1e. Twin Primes Follow up with Pseudocode Primes and Twin Primes
Photo credit : Charles Spackman
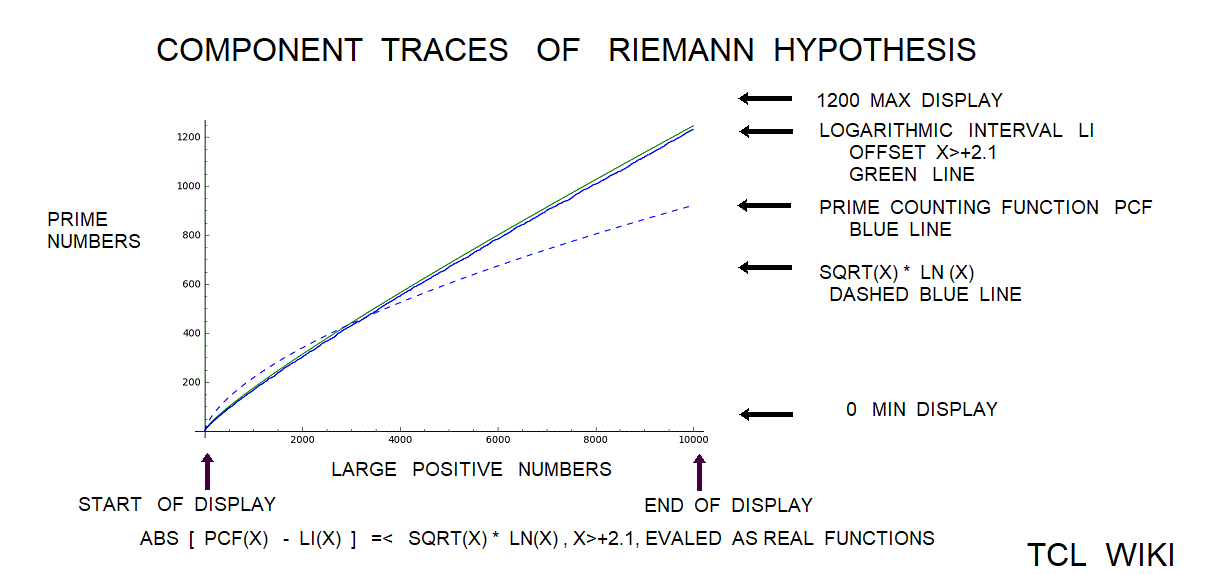
figure 1f. Twin Primes Follow up with Pseudocode Study Gauss Li(x) function
Photo credit : Charles Spackman
Twin Primes Follow up with Pseudocode Study Gauss Li(x) function
figure 2.
figure 3.
figure 4.
figure 5.
figure 6.
figure 7.
figure 8.
figure 9.
figure 10.
figure 11.
figure 12.
The Arakarum Operator Stage is found in some Babylonian Algorithms
gold Update Gist 3/13/2024. While the modern mathematicians are trying to find prime numbers in base_10, the Babylonian mathematicians in base_60 were trying to avoid prime numbers. The primes are the Achilles heel of the Babylonian multiplication system using reciprocals in base_60. The number set in the sequence {7 11 13 14} was especially foul to the Babylonian multiplication system, although the Babylonian mathematicians did use the set {7 11 13 14} in arithmetic or "advanced non-standard" calculations. One trick that the Babylonian mathematicians was to multiply an odd number or prime number by 2 or 3 at one early stage of the calculations and then divide out respectfully the 2 or 3 at a later stage of the calculations. For example, 7*2 converts an overtly prime number to a number 14 with factors 2*7. However, this multiplication trick with 2 or 3 as factors is confusing in the extant school and library tablets, so sometimes the modern reader is stressed by a missing factor of 2/3 after corrupted or dropped tablet lines.
The Arakarum Operator Stage is found in some Babylonian Algorithms like Babylonian Square Root Algorithm, Babylonian Brothers Algorithm, and Babylonian Brothers Algorithm. The Arakarum Operator is also found on some early cuneiform school tablets, the Arakum operator may be more common in cuneiform mathematics than supposed here. Aside from multiple operators for addition and multiplication, the Babylonian mathematicians used the Arakarum math operation. Essentially in reciprocal and algorithm operations, Arakarum means take a take reciprocal of a number N and multiply by another factor usually integer 2, 3, or some other factor, < 2./N1 >. The Arakarum is a combined term of ara for raise or multiply and karum which means factor. In the older texts, the phrases usually was Arakarum 2, Arakarum 3, and Arakarum N1 in the texts. Some example values in modern notation are < 2./N1 >, < 3./N1 >, & < 5./N1 >. But for most cuneiform texts, the factor number in the Arakarum operation was either dropped for abbreviation, assumed to be 2 , or assumed known from context.
For the Arakarum operation, multiplication is associative in that < (1/N1) * 2 = 2* (1/N1) >. So there are instances where the reciprocal is taken first and then multiplied by the factor as well as instances where the factor is applied first and then the reciprocal is taken. Sometimes the Arakarum operation was off the math tablet, so the order of multiplication and reciprocation is not known.
The Babylonian number system in base 60 used regular numbers with factors of < 2,3,5 >, so multiplication by two would assure the number was changed to an even number. Not sure about the entire number line, but multiplication by some factor would ensure the new number was a factorable number and especially not a prime number like 7 or 13. In some of the Babylonian market rate algorithms, the appearance of the Arakarum math operation is striking because there seems no purpose to the modern reader. In most instances, the Arakarum math operation is either factored back out in the line of calculations or else not reported in the answer. Whether caused by a tablet copyist error, line dropped, or scribal mistake, sometimes the Arakarum factor of 2 and other factors was sometimes introduced and not removed. When the Arakum factor was not removed in the text, stressful and very tough on the modern reader for sure, but moderns were not the primary audience.
One possible example where a prime number like 7 or 13 is multiplied by a factor of 2 or 3 could be in the calculation of square roots using the Babylonian method. In the Babylonian square root algorithm, the number is repeatedly averaged with its reciprocal until convergence to the square root is achieved. This process involves taking the reciprocal of the current approximation and multiplying it by a factor, such as 2 or 3, before averaging it with the original number. For instance, if we are calculating the square root of 13 using the Babylonian method, the Arakarum operation may involve taking the reciprocal of 13 and multiplying it by a factor like 3 before averaging it with 13 to update the approximation. This use of a factor like 2 or 3 in the Arakarum operation helps in avoiding prime numbers in the algorithm and facilitates convergence to the square root.
There are a number of "scratch" tablets with three or four columns of numbers which highlight the Arakarum operation. While the Arakarum operation is a mid stage in most Brothers Inheritance problems, believe that additional study on the Arakarum operation may furnish some insights into Babylonian number theory.
Hidden Comments Section
Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Thanks, gold 12Aug2020
test edit
Functional and Imperative Programming Functional programming computes an expression, while imperative programming is a sequence of instructions modifying memory. The former relies on an automatic garbage collector, while the latter requires explicit memory allocation and deallocation. Memory and Execution Control Imperative programming provides greater control over execution and memory representation, but can be less efficient. Functional programming offers higher abstraction and execution safety, with stricter typing and automatic storage reclamation. Historical Perspectives Historically, functional programming was associated with symbolic applications, and imperative programming with numerical applications. However, advances in compiling and garbage collection have improved efficiency and execution safety for both paradigms. The Appeal of Tool Control Language TCL TCL emphasizes that efficiency need not preempt assurance, as long as efficiency remains reasonably good. This approach is gaining popularity among software producers.
gold prompt? Improve, elaborate, explain steps, and explain definitions in numbered steps with numbered steps with details, dates, and elaboration in regard to computer applications, and Tool Control Language TCL ; use titles on each paragraph consisting of 1,2,3 or 4 words? Restrict each paragraph to 30 words or less?
gold prompt? improve, condense, elaborate, explain steps, and explain definitions in numbered steps with numbered steps with details, dates, and elaboration in regard to computer applications, and Tool Control Language TCL ; use titles on each paragraph consisting of 1,2,3 or 4 words? Restrict each paragraph to 30 words or less? Restrict text to third person and impersonal discussion text, substitute one for you, substitute ones for your, use one for he, use ones for his?
..
gold Prompt: improve, condense, elaborate, explain steps, and explain definitions in numbered steps with numbered steps with details, dates, and elaboration in regard to computer applications, and Tool Control Language TCL ; use titles on each paragraph consisting of 1,2,3 or 4 words? Omit blank lines? Restrict each paragraph to 30 words or less? Restrict text to third person and impersonal discussion text, substitute one for you, substitute ones for your, use one for he, use ones for his?
Note. What about all negative values or mixed positive/negative values. Under definitions of arithmetic mean? Under math check. The procedure calculates the mean by summing all values and then dividing the sum by the number of values, regardless of the signs of the values. The arithmetic mean, also known as the average, is calculated by adding up all the values and then dividing the sum by the number of values. This definition applies to all types of values, including negative or mixed positive/negative values. The pseudocode accurately follows this definition by summing all values, regardless of their signs, and then dividing the sum by the number of values.
When calculating the arithmetic mean of a set of values, whether they are all negative, all positive, or a mix of positive and negative values, the process remains the same. The arithmetic mean is calculated by summing all the values and then dividing by the total number of values.
For example, if you have a set of negative values such as (-1, -2, -3), the arithmetic mean would be calculated by adding -1, -2, and -3 together to get -6, and then dividing by 3 (the total number of values) to get an arithmetic mean of -2.
Similarly, if you have a mix of positive and negative values (e.g., 1, -2, 3), you would sum the values (1 + (-2) + 3 = 2) and then divide by 3 to get an arithmetic mean of approximately 0.67.
The arithmetic mean calculation is not affected by the sign of the values, as it is a measure of central tendency that considers the magnitude of the values rather than their sign. ---
# pseudocode
# example to illustrate this process:
# Function to check if a number is prime
function is_prime(n):
if n < 2:
return False
for i from 2 to sqrt(n):
if n % i == 0:
return False
return True
# Function to find twin prime pairs and calculate the gap
function find_twin_primes():
twin_primes = []
for i from 2 to MAX_NUMBER:
if is_prime(i) and is_prime(i + 2):
twin_primes.append((i, i + 2))
prime_gaps = []
for pair in twin_primes:
gap = pair[1] - pair[0]
prime_gaps.append(gap)
return prime_gaps
# Function to calculate the average of prime gaps
function calculate_average(gaps):
total = 0
for gap in gaps:
total += gap
average = total / len(gaps)
return average
# Main program
twin_prime_gaps = find_twin_primes()
average_gap = calculate_average(twin_prime_gaps)
print("Average gap between twin primes: ", average_gap)
proc legendre_tester {limit} { $limit / (log($limit) - 1.08366) }
proc legendre_tester {limit } { expr {$limit / ((log($limit) - 1.08366)*(log($limit) - 1.08366))}}
puts " legendre_tester [ legendre_tester 100 ] "
puts " legendre_tester [ legendre_tester 1000 ] "
puts " legendre_tester [ legendre_tester 10000 ] "
# legendre_tester 8.063843715007492 # approximation
# check proc legendre_tester {limit } { expr {$limit*1.32032 / ((log($limit) - 1.08366)*(log($limit) - 1.08366))}}Here are some references and internet links related to the Babylonian algorithms:
1. Robson, Eleanor. "The Babylonian Mathematical Text cuneiform 46-16-421, an introduction and transliteration".
2. Friberg, Joran. "A Preliminary Survey of Babylonian Algebra and Logical Structures: With Some Clues
##----
Testing Log Approximation for Twin Prime Counting Function
# using mathop here in spots
# legendre_prime_density function might be in mathops.
proc legendre_prime_density_approx {nn} {[/ 1. [- [log $nn 1.0866 ]] ] }
# PI2(n) ~~ n/(log(n)*log(n)
# an estimate for the number of Sophie Germain primes as being roughly 1.32032*N/Log(N)^2.
# the Hardy Littlewood conjecture
# "" for the count of twin primes is “accurate” up to primes of 600 digits."""
# P2(N) < 2*C2*N /(log N)**2, C2=0.6601618158...
# Under test, have to check syntax, that log function is natural log ln, I think.
# expr expression from Tcclib for legendre_tester == expr {$limit / (log($limit) - 1.08366)}
# proc legendre_tester {nn} { expr { 1./ ((log(n)*log(n) ) } }
# proc twin_counting_func_tester {limit} { }
#proc twin_counting_func_tester {nn} { expr { 1./ ( log($nn)* log($nn) ) } }
# expression (1.32032..)n/(log n)^2 from paper of Bertrand Wong
proc twin_counting_func_tester {limit} { expr { ( $limit * 1.32032) / ( log($limit)* log($limit) ) } }
puts " "
puts " twin_counting_func_tester 10 = [ twin_counting_func_tester 10 ] "
puts " twin_counting_func_tester 100 = [ twin_counting_func_tester 100 ] "
puts " twin_counting_func_tester 1000 = [ twin_counting_func_tester 1000 ] "
# Can't duplicate Wong's results, which seem reasonable.Testcases. counting 3 under 10, counting 7 under 20, counting 8 under 30, counting 15 under 100.
# RS on Rational fractions
proc dbl2frac {dbl {eps 0.001}} {
# Set the number of values
set N [expr { [llength $args] + 1 }]
# If only one value, return 0
if {$N == 1} {
return 0
}
for {set den 1} {$den<1024} {incr den} {
set num [expr {round($dbl*$den)}]
if {abs(double($num)/$den - $dbl) < $eps} break
}
set lister []
set lister [list $num $den ]
return $lister
}
puts " dbl2frac = [dbl2frac 0.333 .001]"
puts " dbl2frac = [dbl2frac 1.3063778838630806904686144926 .001] "
# 1.3063778838630806904686144926
puts " dbl2frac = [dbl2frac 1.902160583104 .000000000000001]"dbl2frac = 1 3 dbl2frac = 47 36 47/35 = 1.3055555 dbl2frac = 1336 1024 1336/ 1024 = 1.3046875 dbl2frac = 1946 1024 1946 / 1024 = 1.900390625
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |